二項定理 ・二項係数 :
(a＋b)² を展開すると
(a＋b)² ＝ a²＋2ab＋b²
(a＋b)³ を展開すると
(a＋b)³ ＝ a³＋3a³b＋3ab³＋b³
(a＋b)⁴ を展開すると
(a＋b)⁴ ＝ a⁴＋4a³b＋6a²b²＋4ab³＋b⁴ 　　　
それでは一般に、(a＋b)ⁿ の展開公式はどうなるであろうか。
そこでもう一度 (a＋b)⁴ の展開公式を調べてみる。
(a＋b)⁴ を展開すると、出てくる項は
a⁴, a³b, a²b², ab³, b⁴
の5つである。これらの係数を組合せ _nC_r の考え方を用いて求めてみる。たとえばa³b の項は
(a＋b)⁴ ＝ (a＋b)(a＋b)(a＋b)(a＋b)　⇒　a³b
のように、4個の因数 (a＋b) のうち1個から b を取り出し、残り3個から a を取り出してかけ合わせたものであり、その取り出し方は ₄C₁ 個ある。したがって、a³b の係数は ₄C₁ である。
また、a⁴ はどの因数からも b を取り出さない、すなわち a だけを取り出してかけ合わせたものであるから、その係数は ₄C₀ であり、同様に考えて、a²b², ab³, b⁴ の係数はそれぞれ ₄C₂, ₄C₃, ₄C₄ である。したがって
(a＋b)⁴ ＝ ₄C₀a⁴＋₄C₁a³b＋₄C₂a²b²＋₄C₃ab³＋₄C₄b⁴
と表せる。一般に
(a＋b)ⁿ ＝ (a＋b)(a＋b)(a＋b) … (a＋b)
についても、同じことがいえる。すなわち、展開によって現れる項は
aⁿ, a^n-1b¹, a^n-2b², …, a^n-rb^r, …, ab^n-1, bⁿ
の (n-1) 個である。ここで a^n-rb^r について考えると、n 個の因数 (a＋b) のうちから、b を r 個取り出し、残りの中から a を (n-r) 個とりだしてかけ合わせたものであるから、その取り出し方は、n 個から r 個とる組みあわせの数に等しく、_nC_r 個ある。よって
（a^n-rb^r の係数）＝ _nC_r
これは r ＝ 0, 1, 2, 3, …, n のときつねに成り立つから a⁰ ＝ b⁰ ＝ 1 と定めると、次の等式が成り立つ。

(a＋b)n ＝ nC0an＋nC1an-1b1＋ … ＋ nCran-rbr＋ … ＋ nCnbn

また、�� の知識があれば、次の等式で表せる。

n　 (a＋b)n ＝ �煤@nCkan-kbk k=0

この等式を 二項定理 といい、_nC_ra^n-rb^r を 一般項 という。また、二項定理の右辺の係数 _nC₀, _nC₁, _nC_r, _nC_n
を 二項係数 という。

パスカルの三角形 : 係数の代表的な求め方
　　　

これは (a＋b)ⁿ のそれぞれの係数を表していて、上から n = 0, n = 1, n = 2, n = 3, … となっている。
例えば上から7つ目は n = 6 つまり (a＋b)⁶ の係数を表していて
(a＋b)⁶ ＝ 1a⁶＋6a⁵b＋15a⁴b²＋20a³b³＋15a²b⁴＋6ab⁵＋1b⁶
となる。

多項定理 :
(a＋b＋c)ⁿ や一般の (a＋b＋c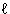＋…＋)ⁿ のように、3つ以上の項からなる式の n 乗の展開式については、二項定理と同様に多項定理が成り立ち
(a＋b＋c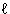＋…＋)ⁿ
の展開式における一般項は

n! / p! q! r! … t! × apbqcr … t 　　　　　　　　　　　　　(p＋q＋r＋…＋t = n ； p, q, r, …, t は負でない整数)

である。

戻る